This document is relevant for: Inf1, Inf2, Trn1, Trn2, Trn3

Intra-node Collective Communications with AWS Neuron

This topic covers intra-node collective communication algorithms and optimization strategies for AWS Neuron distributed workloads within a single node. It examines Ring, Mesh, KangaRing, and Recursive Doubling-Halving (RDH) algorithms for coordinating data exchange between NeuronCores connected via high-bandwidth intra-chip and chip-to-chip NeuronLink interconnects.

Overview

Intra-node collective communication enables efficient data exchange between NeuronCores within a single physical node or tightly coupled nodes connected via NeuronLinks. This document explores four primary algorithmic approaches—Ring, Mesh, KangaRing, and RDH—each optimized for different message sizes and latency requirements. The algorithms leverage the 2D Torus topology of Trainium chips and specialized hardware features like duplication to minimize memory bandwidth pressure and maximize throughput.

Applies to

This concept is applicable to:

• Distributed Training: Collective communication aggregates and synchronizes gradients across workers to maintain model consistency. In this scenario, collective operations enable workers to compute gradient sums across all nodes, ensuring uniform parameter updates.

• Distributed Inference: During inference, collective communication distributes requests across multiple accelerators in serving nodes, optimizing resource utilization and maintaining low latency under high loads.

Collective Communication Operations

We define the following denotations:

• N: the number of participating ranks in a communication group

• C: a “chunk”, which is a piece of data (subset of tensor data transmitted at each algorithm step) with size equaling to that of a rank’s input in AllGather, or output in ReduceScatter

• B: the size of both the input and output buffer in AllReduce. In that context, C = B / N

Now we establish the following collective operations:

Table 5 Collective Operations

Operation Type	Input Size	Output Size	Explanation
AllGather	C	N * C	Each rank starts with a chunk and ends with everyone else’s chunks
ReduceScatter	N * C	C	Each rank starts with N chunks, and ends with a unique chunk which is fully reduced among the N ranks
AllReduce	B = N * C	B = N * C	Each rank contributes B, and ends with B which is fully reduced among the N ranks. AllReduce can be seen as a concatenation of ReduceScatter followed by AllGather
AllToAll	B = N * C	B = N * C	Each rank starts with N chunks, and ends with the N in a way that the pieces of data were transposed between the ranks r0[A0, A1] r1[B0, B1] → r0[A0, B0], r1 [A1, B1]

The execution time of a collective communication operation consists of two portions: latency + data transfer time. More concretely, the latency term is of 10^0 to 10^1 us magnitude. For example, the per-hop latency of Ring/KangaRing is about 1-2 us (HBM load dependent). On the other hand, the transfer time is dependent on the buffer/message size. For example, to transfer 1KB, 1MB, and 1GB at 100GBps takes 10 ns, 10 us, and 10 ms respectively. Therefore, the collective communication problem is latency dominant for small sizes, and throughput dominant for large sizes, and a balance for mid-sizes. For this reason, different strategies and algorithms are required to provide the best performance for each range.

Ring Algorithm

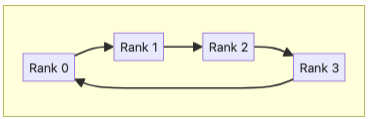
In Ring algorithm, all the ranks are connected in a directed cycle. Algorithmically, it has O(N) per-hop latency where N is the number of ranks. In practice, we run multiple cycles with mutually exclusive wires in parallel for full wire bandwidth. That means big tensors (packets) are divided into smaller packets called chunks (more specifically, a chunk is a subset of tensor data transmitted at each algorithm step. The chunk size depends on number of participating ranks on collective) that are transferred across ranks in one or more cycles.

Ring AllGather

In step 0, each rank sends its input chunk to its downstream neighbor. In step 1, each rank sends the chunk it has just received from upstream to downstream. The process goes on until all the chunks have traversed the ring.

Ring ReduceScatter

In step 0, each rank r sends its (r-1)th chunk to its downstream. In step 1, each rank reduces the chunk it has just received with the same indexed chunk from its own input, and writes the result to downstream. The process goes on until each rank has its output chunk fully traversed the ring. It is important to mention a chunk transmit is divided into two sliced transmissions, where the first slice reduction overlaps the second slice communication.

Ring AllReduce

This algorithm is a concatenation of the above two patterns (ReduceScatter followed by AllGather), so it requires the ring to be traversed twice.

Mesh Algorithm

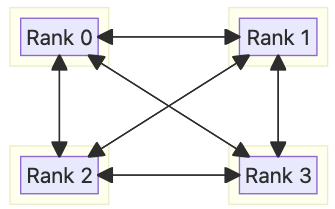
The Mesh algorithm aims to optimize latency for small message sizes. Rather than transferring data step-by-step like in Ring and accumulate per-hop latency along the way, Mesh directly broadcasts/scatters data to all other ranks in one step, hence, to a first degree it has O(1) latency. This is made possible by inter-chip routing — from a rank, data can be directly written to any other rank on a remote chip, where the in-between traffic is routed automatically. The downside of routing is that it leads to link over-subscription, hence mesh is good for mainly small sizes.

Mesh AllGather

This algorithm consists of two steps. In step 0, each chip contains 4 input chunks which need to be broadcasted to the other 15 chips. We split these destinations roughly evenly among the 4 local ranks. Each rank reads the 4 chunks, either locally or over intra-chip connectivity, and writes to the closest rank on each destination chip via routing. In step 1, each local rank has received 16 distinct chunks. We then run intra-chip broadcast to further exchange them.

Mesh ReduceScatter

This algorithm also involves two steps. In step 0, each rank is tasked to send to roughly a quarter of the other 60 off-chip ranks. For each destination, the local rank reads 4 on-chip chunks, one from each NeuronCore (LNC=1 or LNC=2), which correspond to the destination rank, reduces them, and writes the result over via routing. In step 1, each rank has received 16 partially reduced chunks, each of which is from a different chip. It then reads these 16 chunks, reduces them, and writes the result to output.

Mesh AllReduce

This algorithm is a concatenation of the above two patterns (ReduceScatter followed by AllGather).

Single-step Mesh Algorithm (AllReduce)

The Single-step Mesh algorithm is a variant of Mesh specifically designed for AllReduce. The goal is to trade off bandwidth optimality for a reduced number of hops (from 2 to 1). Rather than simply concatenating ReduceScatter and AllGather, we can have each rank duplicate and broadcast its whole input buffer to all peers. Upon receiving these duplicates, a rank will reduce the whole buffer to its output.

KangaRing Algorithm

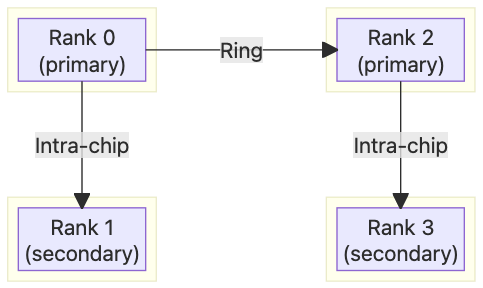
The KangaRing Algorithm is an extension and optimization of Ring. Rather than connecting all ranks in a flat cycle, we group each two ranks (with LNC=2 each rank is composed of 2 NeuronCores) out of four on the same Neuron Device, nominate one as primary and the other as secondary, and connect only the primary ranks in a cycle. Hence, the per-hop latency is cut by half when compared with Ring (although still O(N)). Primary ranks handle all the data movement and reduction, while secondary ranks just sit idle. In practice, we will alternate the assignment of primary and secondary ranks in different cycles (when using all 16 Neuron Devices, there are 2 non-overlapping Hamiltonian cycles on 2D Torus), so that each rank is active in half of them.

KangaRing AllGather

Algorithm-wise, in step 0, each primary rank sends its self chunk as well as the secondary chunk to the downstream. In subsequent steps, it reads the newly received chunk and duplicates it to both the secondary peer and downstream. Duplication is a hardware feature that allows a data transfer to only incur one read but duplicate the write to two destinations, for reduced HBM pressure. Specifically, for each chunk to traverse every 2 ranks, Ring needs to do 1R1W (one read / one write) twice, resulting in 4 HBM accesses. The same transfer can be done with one 1R2W (one read / 2 writes) in KangaRing, resulting in 3 HBM accesses or a 25% reduction.

KangaRing ReduceScatter

In step 0, each primary rank reduces self and secondary chunks and writes the result to downstream. In subsequent steps, it reduces the newly received partial sum, self chunk, and secondary chunk, and writes to downstream. For each chunk to traverse every 2 ranks, Ring needs to do 2R1W (two reads / 1 write) twice, resulting in 6 HBM accesses. In comparison, KangaRing does one 3R1W for only 4 touches or a 33% reduction.

KangaRing is an option for TP replica-groups where all ranks in device are in same rank-list. For instance: On a one-rank-per-chip rank-list replica-group, Ring is used rather than KangaRing. In these particular cases, KangaRing is better than Ring at all sizes. At smaller sizes, it has better latency. At larger sizes, which are HBM bandwidth bound or contended, the number of touches is reduced. But obviously, it still loses to Mesh at small sizes. KangaRing is only relevant for TP replica-groups where all ranks in chip are in same rank-list.

Recursive Doubling and Halving (RDH) Algorithm

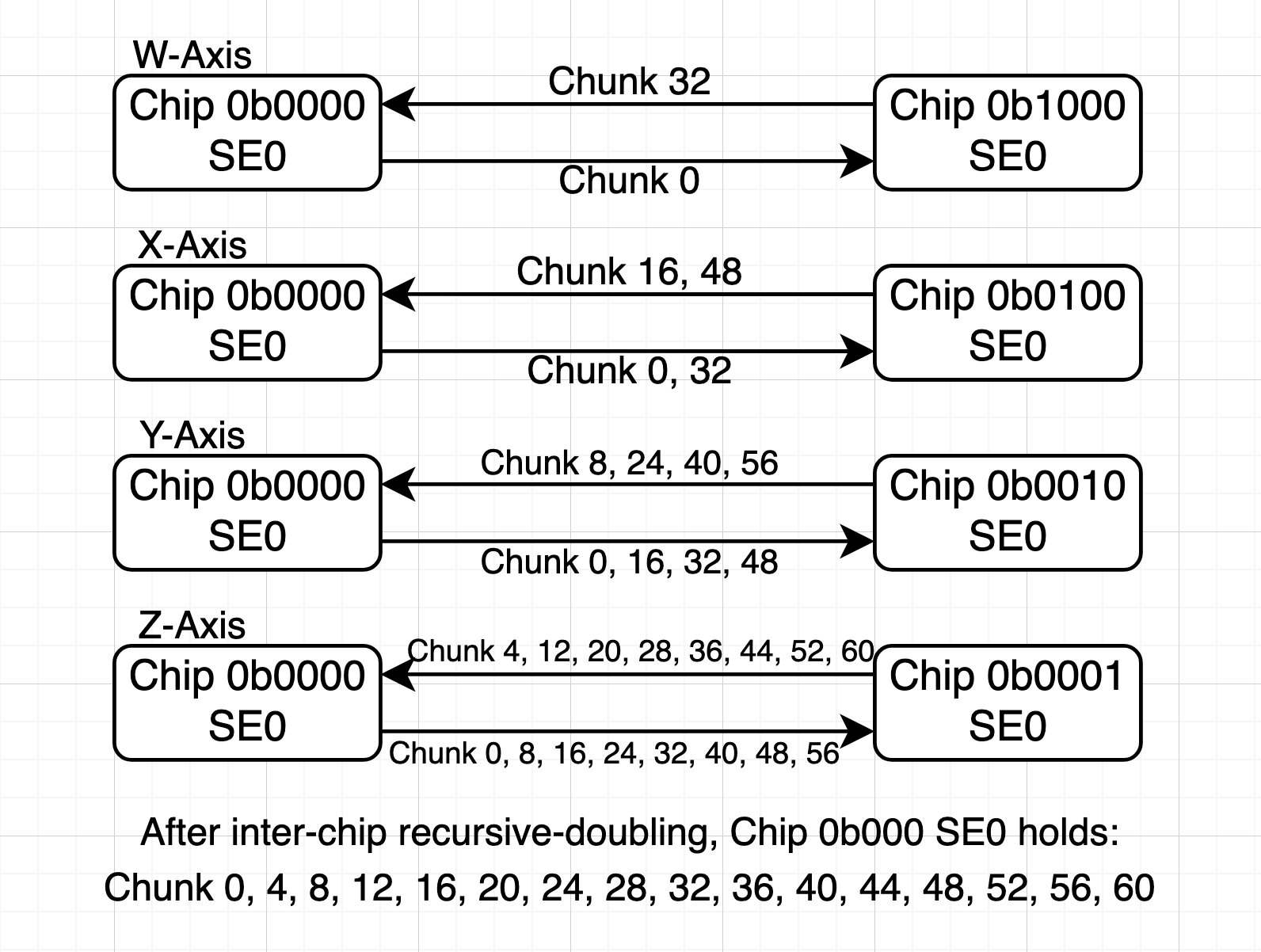
The RDH Algorithm optimizes for mid-size collectives, where both the latency and transfer factors matter. The 2D-Torus connectivity can also be seen as a 4D hyper-cube, where each Chip can reach to a neighbor in 4 axis directions W, X, Y, and Z.

RDH AllGather

This algorithm involves two stages: inter-chip recursive-doubling and intra-chip broadcast. In the first stage, ranks of the same in-chip index form a communication group, so there are 4 groups of 16 ranks each. Within a group, each rank sends/receives in the 4 axis directions sequentially, and pair-wise exchanges the received chunks so far. By the end of recursive doubling, chunks within each communication group are fully broadcasted. In the second stage, intra-chip broadcast, the 4 local ranks then use intra-chip to further exchange chunks.

RDH ReduceScatter

The algorithm also involves two stages: intra-chip reduction and inter-chip recursive halving. In the first stage, a quarter of the chunks are partially reduced to each of the 4 local ranks, with indices corresponding to each rank’s inter-chip communication group members. In the second stage, each rank sends/receives the partially reduced chunks in the 4 axis directions sequentially, halving its problem space at each step, until there is one fully reduced chunk left.

Evidently, the intra-chip stage has O(1) number of steps or latency, and the inter-chip recursive stage has O(logN) latency, where N is the number of ranks. When a rank communicates in an axis direction that requires on-chip routing via intra-chip, it may contend with traffic by another rank, but this only happens in some of the cases. So, RDH suffers from less severe link over-subscription than Mesh.

Algorithm Summary

Table 6 Algorithm Comparison

Algorithm	Latency	Link Utilization	HBM Pressure	Sweet Range (Empirically)
Ring	O(N)	Full	Normal	Fallback only
Mesh	O(1)	Over-subscription	Normal	< 1MB
RDH	O(logN)	Partial Over-subscription	Normal	1-56MB
KangaRing	O(N/2)	Full	Reduced	>56MB

More information

• Inter-node Collective Communications

• About Neuron Runtime Collectives

This document is relevant for: Inf1, Inf2, Trn1, Trn2, Trn3