This document is relevant for: Inf2, Trn1, Trn1n

Tensor Parallelism Overview

Tensor Parallelism is a technique in which a tensor is split into N chunks along a particular dimension such that each device only holds 1/N chunk of the tensor. Computation is performed using this partial chunk so as to get partial output. These partial outputs are collected from all devices ensuring the correctness of the computation is maintained.

Taking a general matrix multiplication as an example, let’s say we have C = AB. We can split B along the column dimension into [B0 B1 B2 … Bn] and each device holds a column. We then multiply A with each column in B on each device, we will get [AB0 AB1 AB2 … ABn]. At this moment, each device still holds partial results, e.g. device rank 0 holds AB0. To make sure the result is correct, we need to all-gather the partial result and concatenate the tensor along the column dimension. In this way, we are able to distribute the tensor over devices while making sure the computation flow remains correct.

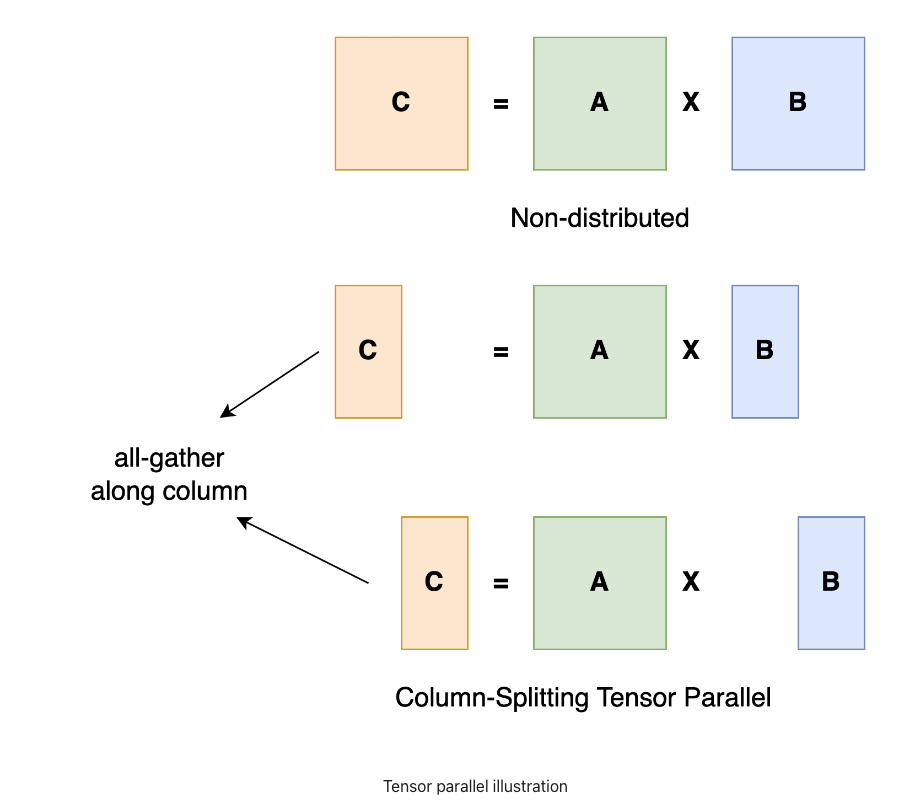
Fig and TP explanation is borrowed from https://colossalai.org/docs/concepts/paradigms_of_parallelism/#tensor-parallel

Similarly we can perform the partition along the row dimensions and create a RowParallel Linear layer. In RowParallelLinear layer, we partition the weight matrix along the row dimension. Let’s say we have C = AB. We can split B along the row dimension into [B0 B1 B2 … Bn] and each device holds a row. We then multiply each column of A on each device, we will get [A0B0 A1B1 A2B2 … AnBn]. At this moment, each device still holds partial results, e.g. device rank 0 holds A0B0. To make sure the result is correct, we need to all-reduce sum the partial result from all devices to produce the final output.

Using this principle of sharded linear layers, we can construct MLPs of arbitrary depth until the need to operate on the whole output tensor, in which case we would have to construct the output but gathering it from all devices.

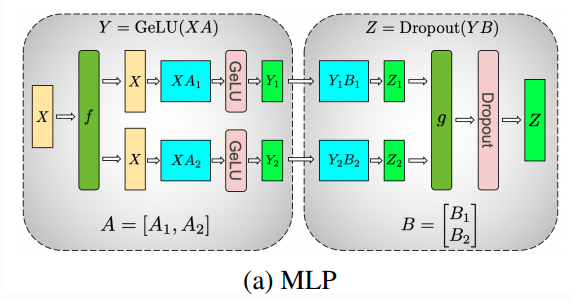
Here is an illustration from the Megatron-LM paper In the above case, as you can see two linear layers are implemented using Column Parallel and Row Parallel linear layers, wherein the ColumnParallel Linear shards along the columns and then it is followed by RowParallel Linear layer which takes in parallel inputs (sharded outputs from ColumnParallelLinear). Consider the example shown in the above diagram, Z = (XA)B. In this case we split the first matrix multiplication over column dimension such that each device after first matrix multiplication holds partial result of Y0=XA0,Y1=XA1 and so on. For the second matrix multiplication, we partition the weight matrix over row dimension and since the inputs are already columns sharded and we can multiply them to produce partial outputs. These outputs finally requires an all-reduce sum, since we want to sum up the single column*row result.

Tensor Parallelism for Transformers:

A transformer block

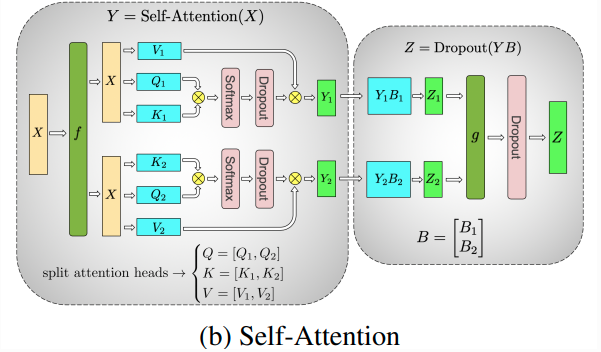
Fig: Taken from Megatron-LM paper.

As seen from the figure above, a simple self attention block has the QKV linear layer followed by MLP. Using the same Column and Row Parallel linear layers, we can partition the self-attention block across devices thereby reducing the memory footprint on each device, since each device now only holds partial parameters. This weight distribution strategy allows us to scale large model training across devices.

This document is relevant for: Inf2, Trn1, Trn1n