Tensor Indexing on NKI

This topic covers basic tensor indexing and how it applies to developing with the AWS Neuron SDK. This overview describes basic indexing of tensors with several examples of how to use indexing in NKI kernels.

Basic Tensor Indexing

NKI supports basic indexing of tensors using integers as indexes. For example, we can index a 3-dimensional tensor with a single integer to get get a view of a portion of the original tensor.

x = nl.ndarray((2, 2, 2), dtype=nl.float32, buffer=nl.hbm)

# `x[1]` return a view of x with shape of [2, 2]
# [[x[1, 0, 0], x[1, 0 ,1]], [x[1, 1, 0], x[1, 1 ,1]]]
assert x[1].shape == [2, 2]

NKI also supports creating views from sub-ranges of the original tensor dimension. This is done with the standard Python slicing syntax. For example:

x = nl.ndarray((2, 128, 1024), dtype=nl.float32, buffer=nl.hbm)

# `x[1, :, :]` is the same as `x[1]`
assert x[1, :, :].shape == [128, 1024]

# Get a smaller view of the third dimension
assert x[1, :, 0:512].shape == [128, 512]

# `x[:, 1, 0:2]` returns a view of x with shape of [2, 2]
# [[x[0, 1, 0], x[0, 1 ,1]], [x[1, 1, 0], x[1, 1 ,1]]]
assert x[:, 1, 0:2].shape == [2, 2]

When indexing into tensors, NeuronCore offers much more flexible memory access in its on-chip SRAMs along the free dimension. You can use this to efficiently stride the SBUF/PSUM memories at high performance for all NKI APIs that access on-chip memories. Note, however, this flexibility is not supported along the partition dimension. That being said, device memory (HBM) is always more performant when accessed sequentially.

Tensor Indexing by Example

In this section, we share several use cases that benefit from advanced memory access patterns and demonstrate how to implement them in NKI.

Case #1 - Tensor split to even and odd columns

Here we split an input tensor into two output tensors, where the first output tensor gathers all the even columns from the input tensor, and the second output tensor gathers all the odd columns from the input tensor. We assume the rows of the input tensors are mapped to SBUF partitions. Therefore, we are effectively gathering elements along the free dimension of the input tensor. Fig. 112 below visualizes the input and output tensors.

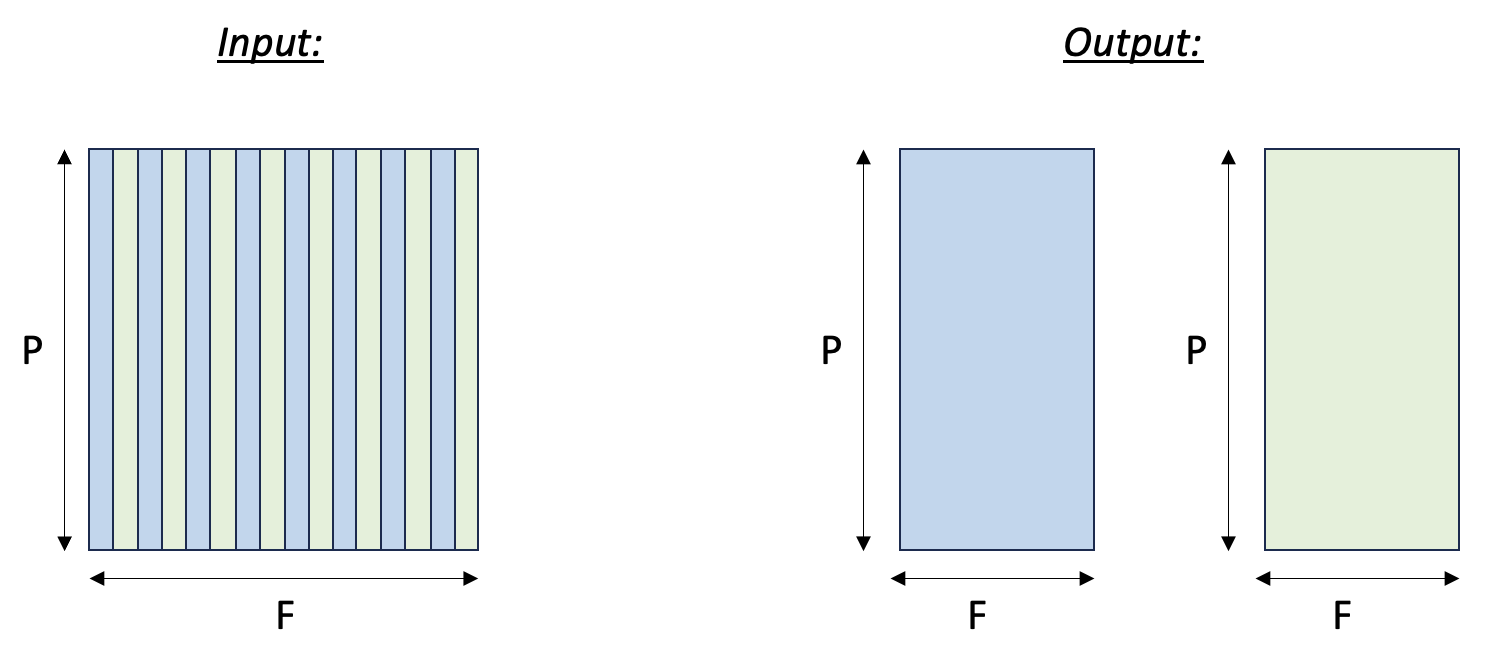
Fig. 16 Tensor split to even and odd columns

from neuronxcc import nki
import neuronxcc.nki.language as nl
import math

@nki.jit
def tensor_split_kernel_(in_tensor):
  """NKI kernel to split an input tensor into two output tensors, along the column axis.

  The even columns of the input tensor will be gathered into the first output tensor,
  and the odd columns of the input tensor will be gathered into the second output tensor.

  Args:
      in_tensor: an input tensor
  Returns:
      out_tensor_even: a first output tensor (will hold the even columns of the input tensor)
      out_tensor_odd: a second output tensor (will hold the odd columns of the input tensor)
  """

  # This example only works for tensors with a partition dimension that fits in the SBUF
  assert in_tensor.shape[0] <= nl.tile_size.pmax

  # Extract tile sizes.
  sz_p, sz_f = in_tensor.shape
  sz_fout_even = sz_f - sz_f // 2
  sz_fout_odd = sz_f // 2

  # create output tensors
  out_tensor_even = nl.ndarray((sz_p, sz_fout_even), dtype=in_tensor.dtype, buffer=nl.shared_hbm)
  out_tensor_odd = nl.ndarray((sz_p, sz_fout_odd), dtype=in_tensor.dtype, buffer=nl.shared_hbm)

  # Load input data from external memory to on-chip memory
  in_tile = nl.load(in_tensor)

  # Store the results back to external memory
  nl.store(out_tensor_even, value=in_tile[:, 0:sz_f:2])
  nl.store(out_tensor_odd,  value=in_tile[:, 1:sz_f:2])

  return out_tensor_even, out_tensor_odd


if __name__ == "__main__":
    import torch
    from torch_xla.core import xla_model as xm

    device = xm.xla_device()

    X, Y = 4, 5
    in_tensor = torch.arange(X * Y, dtype=torch.bfloat16).reshape(X, Y).to(device=device)

    out1_tensor, out2_tensor = tensor_split_kernel_(in_tensor)
    print(in_tensor, out1_tensor, out2_tensor)

The main concept in this example is that we are using slices to access the even and odd columns of the input tensor. For the partition dimension, we use the slice expression :, which selects all of the rows of the input tensor. For the free dimension, we use 0:sz_f:2 for the even columns. This slice says: start at index 0, take columns unto index sz_f, and increment by 2 at each step. The odd columns are similar, except we start at index 1.

Case #2 - Transpose tensor along the f axis

In this example we transpose a tensor along two of its axes. Note, there are two main types of transposition in NKI:

1. Transpose between the partition-dimension axis and one of the free-dimension axes, which is achieved via the nki.isa.nc_transpose API.

2. Transpose between two free-dimension axes, which is achieved via a nki.isa.dma_copy API, with indexing manipulation in the transposed axes to re-arrange the data.

In this example, we’ll focus on the second case: consider a three-dimensional input tensor [P, F1, F2], where the P axis is mapped to the different SBUF partitions and the F1 and F2 axes are flattened and placed in each partition, with F1 being the major dimension. Our goal in this example is to transpose the F1 and F2 axes with a parallel dimension P, which would re-arrange the data within each partition. Fig. 113 below illustrates the input and output tensor layouts.

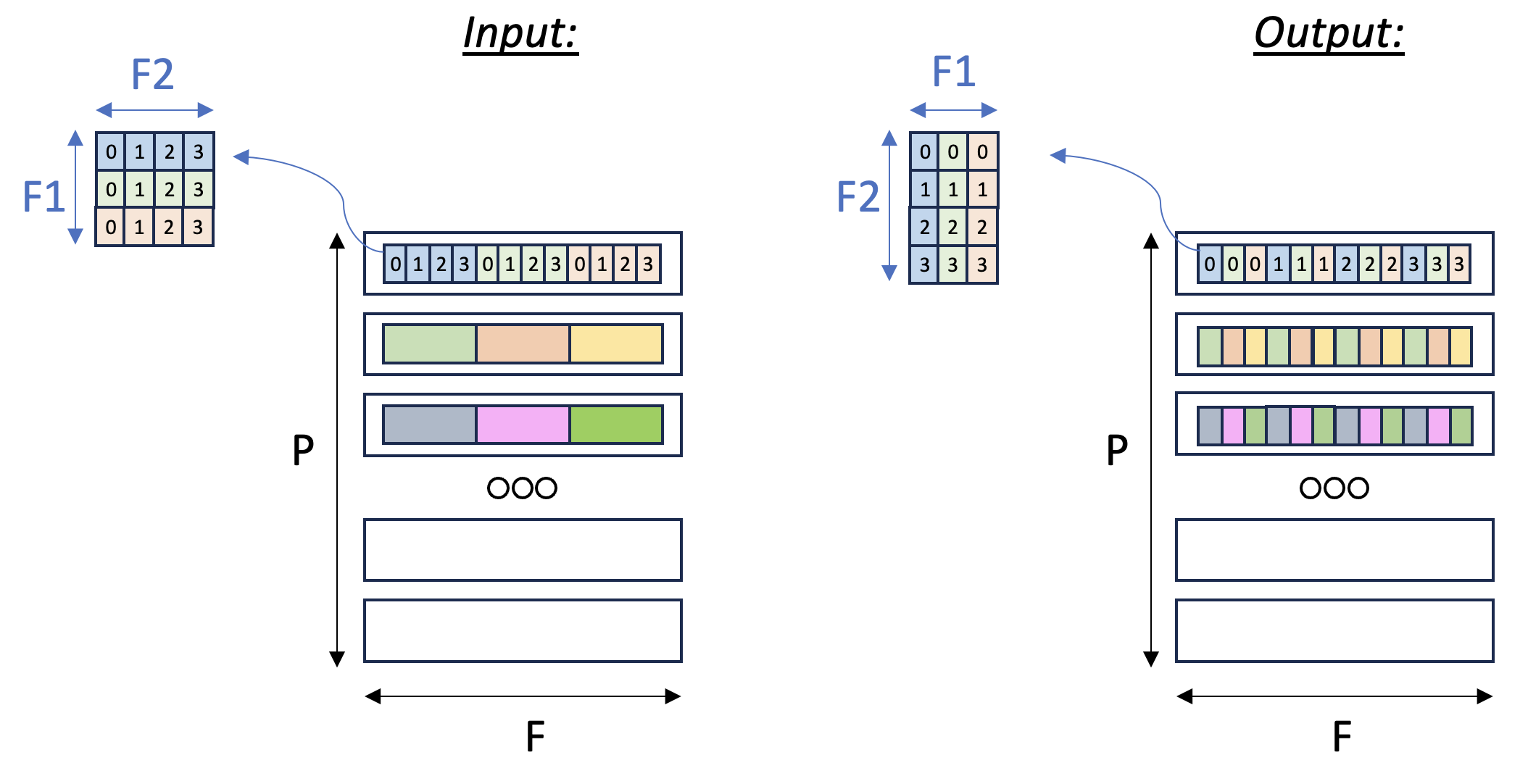
Fig. 17 Tensor F1:F2 Transpose

import neuronxcc.nki as nki
import neuronxcc.nki.language as nl


@nki.jit
def tensor_transpose2D_kernel_(in_tensor, shape2D):
  """
  NKI kernel to reorder the elements on axis[1] of the input tensor.

  Every row of the input tensor is a flattened row-major 2D matrix.
  The shape2D argument defines the dimensions of the flattened matrices (#rows,#cols).
  Our goal in this kernel is to transpose these flattened 2D matrices, i.e. make them (#cols,#rows).

  Example:
      in_tensor = [a0,a1,a2,a3,b0,b1,b2,b3,c0,c1,c2,c3]
      shape2D = (3,4)
  this means that in_tensor has 3 rows and 4 columns, i.e. can be represented as:
      [a0,a1,a2,a3]
      [b0,b1,b2,b3]
      [c0,c1,c2,c3]
  after transpose, we expect to get:
      [a0,b0,c0]
      [a1,b1,c1]
      [a2,b2,c2]
      [a3,b3,c3]
  Thus, out_tensor is expected to be [a0,b0,c0,a1,b1,c1,a2,b2,c2,a3,b3,c3]

  Args:
    in_tensor: an input tensor
    shape2D: tuple representing the dimensions to be transposed: (#rows, #cols)
    out_tensor: an output (transposed) tensor
  """
  out_tensor = nl.ndarray(in_tensor.shape, dtype=in_tensor.dtype,
                          buffer=nl.shared_hbm)
  # Gather input shapes
  sz_p, _ = in_tensor.shape

  # Load input data from external memory to on-chip memory
  in_tile = nl.load(in_tensor)

  # Performing f1/f2 transpose
  # ==========================
  # The desired transpose pattern is provided as an input:
  sz_f1, sz_f2 = shape2D

  # We're going to need 3 indices to perform f1:f2 transpose.
  # - i_p0 is the parallel index
  # - i_f1 and i_f2 are both free-dim indices, and will be used to transpose between the f1/f2 axes
  i_p0, i_f1, i_f2 = nl.mgrid[:sz_p, :sz_f1, :sz_f2]

  # Perform the transposition via a SBUF-to-SBUF copy, with access-pattern manipulation
  # Note that we have 2D tensors and 3 indices, since we need to represent a 2D access pattern *per partition*
  # RHS traverses an F1 x F2 matrix in a row major manner
  # LHS traverses an F2 x F1 (new) matrix in a row major manner
  out_tile = nl.ndarray(shape=(sz_p, sz_f2*sz_f1), dtype=out_tensor.dtype)
  out_tile[i_p0, i_f2*sz_f1+i_f1] = nl.copy(in_tile[i_p0, i_f1*sz_f2+i_f2])

  # Finally, we store out_tile to external memory
  nl.store(out_tensor, value=out_tile)

  return out_tensor

The main concept introduced in this example is a 2D memory access pattern per partition, via additional indices. We copy in_tile into out_tile, while traversing the memory in different access patterns between the source and destination, thus achieving the desired transposition.

You may download the full runnable script from Transpose2d tutorial.

Case #3 - 2D pooling operation

Lastly, we examine a case of dimensionality reduction. We implement a 2D MaxPool operation, which is used in many vision neural networks. This operation takes C x [H,W] matrices and reduces each matrix along the H and W axes. To leverage free-dimension flexible indexing, we can map the C (parallel) axis to the P dimension and H/W (contraction) axes to the F dimension. Performing such a 2D pooling operation requires a 4D memory access pattern in the F dimension, with reduction along two axes. Fig. 114 below illustrates the input and output tensor layouts.

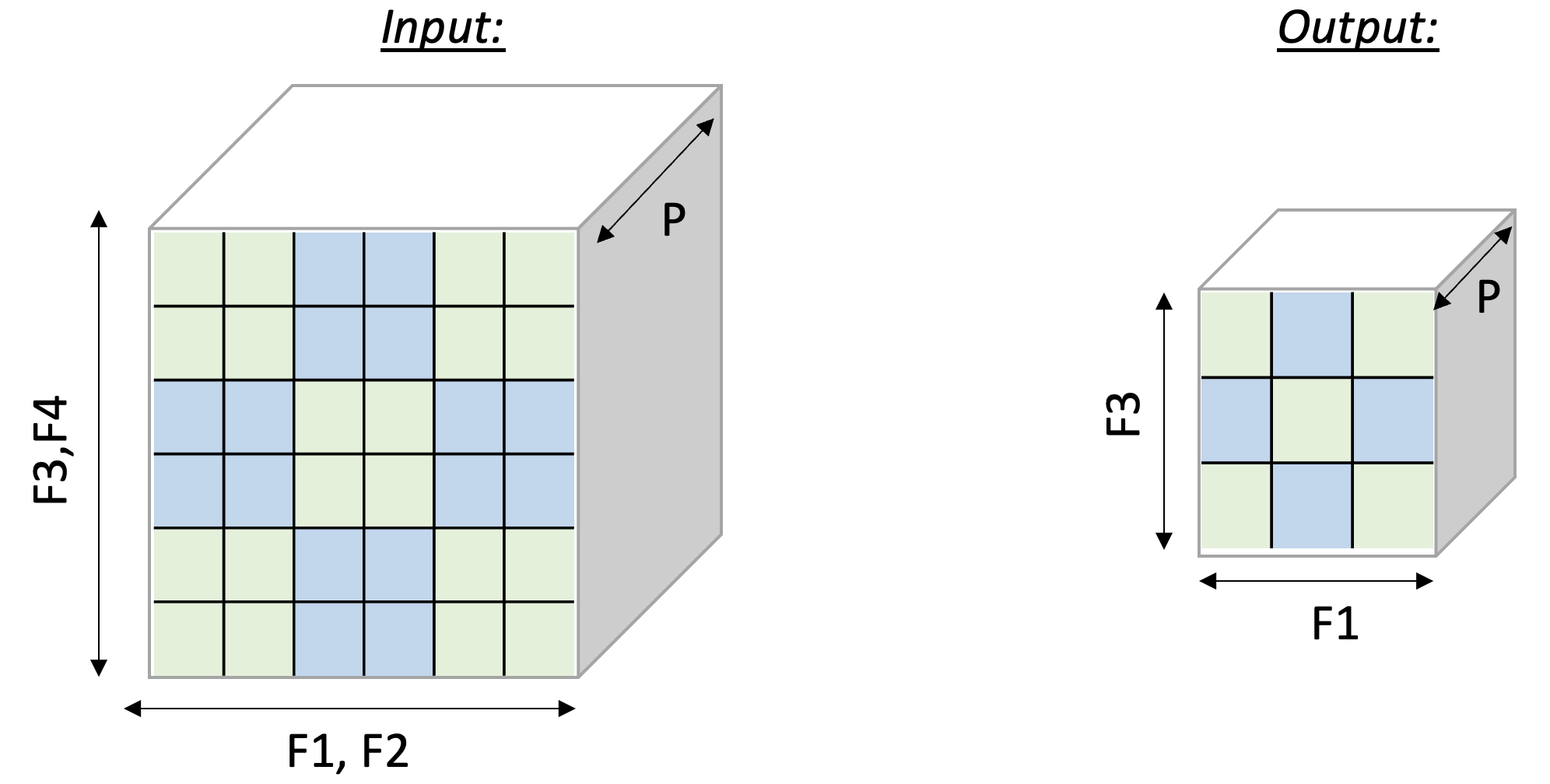
Fig. 18 2D-Pooling Operation (reducing on axes F2 and F4)

from neuronxcc import nki
import neuronxcc.nki.language as nl

@nki.jit
def tensor_maxpool_kernel_(in_tensor, sz_pool):
  """NKI kernel to compute a 2D max-pool operation

  Args:
      in_tensor: an input tensor, of dimensions C x H x W
      sz_pool: integer P representing a (square) pool-window size
  Returns:
      out_tensor: the resulting output tensor, of dimensions C x (H/P) x (W/P)
  """

  # Get input/output dimensions
  sz_p, sz_hin, sz_win = in_tensor.shape
  sz_hout, sz_wout = sz_hin // sz_pool, sz_win // sz_pool
  out_tensor = nl.ndarray((sz_p, sz_hout, sz_wout), dtype=in_tensor.dtype,
                          buffer=nl.shared_hbm)

  # Generate pool index patterns (requires two extra dimensions, for the pool window)
  i_0, i_1, i_2, i_3, i_4 = nl.mgrid[:sz_p, :sz_hout, :sz_pool, :sz_wout, :sz_pool]

  # Load input data from external memory to on-chip memory
  # Declare ndarray to force a 3D tensor (temporary requirement)
  in_tile = nl.ndarray((sz_p, sz_hin, sz_win), dtype=in_tensor.dtype)
  in_tile[...] = nl.load(in_tensor)

  # Perform the pooling operation:
  # We use advanced indexing, in order to extend in_tile to 5D, and then reduce-max two dimension.
  # axis[0] is the index for p_dim, and thus doesn't participate in the reduction operation.
  # axis[1] and axis[2] together index the rows, with axis[2] responsible for inner strides
  # (i.e. inside a pooling window), and axis[1] responsible for the outer strides. As such, we reduce over axis[2].
  # Similarly, axis[3] and axis[4] together index the columns, and we thus reduce over axis[4].
  out_tile = nl.max(in_tile[i_0, sz_pool*i_1+i_2, sz_pool*i_3+i_4], axis=[2,4])

  # Store the results back to external memory
  nl.store(out_tensor, value=out_tile)

  return out_tensor


if __name__ == "__main__":
    import torch
    from torch_xla.core import xla_model as xm

    device = xm.xla_device()

    # Now let's run the kernel
    POOL_SIZE = 2
    C, HIN, WIN = 2, 6, 6
    HOUT, WOUT = HIN//POOL_SIZE, WIN//POOL_SIZE

    in_tensor = torch.arange(C * HIN * WIN, dtype=torch.bfloat16).reshape(C, HIN, WIN).to(device=device)
    out_tensor = tensor_maxpool_kernel_(in_tensor, POOL_SIZE)

    print(in_tensor, out_tensor) # an implicit XLA barrier/mark-step